M454: Intro Dynamical Systems I

       la
 
INSTRUCTOR
  
Mark Pernarowski
 
OFFICE HOURS
  
Schedule
  TEXTBOOK:  
Nonlinear Dynamics and Chaos, Steven Strogatz, 2nd ed.
  GRADE:  
The course % will be determined as follows:
     
                         Percent       Date 
 
Midterm
 
M
25%
  Oct 21 in class
 
Final
 
F
25%
  12/16 @8-9:50am
 
Homework
 
HW
50%
see  HW1-HW5
 
 
 
 
100
  
     

Homework assignments will have different raw scores.

The HW % above is obtained from the sum of the raw scores.

Dates and details for the Midterm and Final exam will be

announced later in the course.

 

All grades will be recorded in D2L.

 
       
  HOMEWORK:  
Below the Homework and due dates will be posted.

 

               Due Date   
                    
   
  HW1
             Thursday, Sept 16
  
   
  HW2
    Thursday, Sep 30
  
      HW3    Thursday, Oct 14  
      HW4   Thursday, Nov 4  
      HW5    Thursday, Dec 2  
           
    FINAL    Thursday Dec 16 (8-9:50am in class)  
     
 
  NOTES   

      Handwritten and/or typeset lecture notes here:

 
     Notes_0        Dynamical system examples, overview, systems, ode, Maps, PDE's and terminology
     Notes_1    First order ODE: stability and phase portraits
     Notes_2a    First Order ODE: existence theorems, blowup, Picard iteration, Taylor Series
     Notes_2b    Linear Stability for fixed points
     Notes_3    Comparison Theorem and Potential Functions
     Notes_4    Saddle and Transcritical Bifurcations
     Notes_5    Pitchfork bifurcations and Structural Stability
     Notes_6    Taylor Series, Implicit Function Theorem, Hyperbolicity, Normal Forms
     Notes_7    Perturbed TC and PF bifurcations and Budworm Population Model
     Notes_8    Dynamics on S1 (unit circle) brief overview
     Notes_9    Planar system notation, fixed point and stability definitions
     Notes_10    Brief review of linear algebra
     Notes_11    Linear planar systems: saddles,nodes,spirals,centers,line of equilibria
     Notes_12    Linear planar systems: classification and manifolds E^s, E^c and E^u (and here)
     Notes_13    Planar systems: nullclines, linearization,hyperbolicity,flow, H-G Theorem
     Notes_14    W^s,W^u, homo/heteroclinic orbits, Lotka Volterra, Conservative & Hamiltonians
     Notes_15    Nonlinear centers and Hamiltonian systems, Reversible systems
     Notes_16     Index Theory
     Notes_17    Polar coord, limit cycles, periods, gradient sys., dissipation, Liapunov fns.
     Notes_18    Dulac Criterion
     Notes_19    Poincare-Bendixson: positive invariance, trapping regions, omega-limit sets
     Notes_19a    Poincare application to Glycolosis Oscillator model
     Notes_20    Relaxation Oscillations: Period estimates
     Notes_21    Bifurcations of Fixed points
     Notes_22    Hopf Bifurcations. Summary notes here
     Notes_23    Global Bifurcations of Periodic Orbits and Return Maps
       
 
MORE NOTES
 
  

Here are some supplementary notes I may refer to:    Book.pdf
 

 

    
  EXAMS:  
    Midterm 1:  (in class, date: Thursday Oct 21 - in class.)
     
     
1)       

Is open notes. You may bring any handwritten or typed notes but not the text.

You may not use software on your computer or phone.

The last page of the exam includes this List of bifurcation Theorems
2)   You won't need scrap paper. You will answer questions on the exam iteself.
3)   You'll need to know basic definitions and SN/TC/PF bifurcations for one T/F question.
4)   The bulk of the exam will be taken from HW-HW3
5)  

Topics included and excluded:

  1. existence and uniqueness questions
  2. phase portraits of x'=f(x) - definitely
  3. Picard iteration - possibly
  4. Taylor series approximations of x'=f(x) - possibly
  5. Potential functions
  6. All definitions of Stability of fixed points - definitely
  7. Definition of hyperbolic points f=0, f_x=0 - definitely
  8. Saddle Node (SN), Transcritical (TC) and Pitchfork bifurcations - definitely
  9. Taylor series approximations for f(x,mu) near non-hyperbolic points- definitely
  10. Locus of nonhyperbolic in (mu,lambda)-plane - possibly (but nothing more than the locus, i.e., not the bifurcations of x, drawing 3-d surfaces. just whats on  homework 3)
       
     
    Final Exam  - (takehome, Due: TBA)
     
1)   Topics: TBA
2)          You may only use the text, your class notes or the online notes.
3)   You may use software for drawing functions curves
4)   You may not talk to any fellow students
5)   You may ask me to clarify questions
       
       
       
  TOPICS:  
    • Dynamics on R
      • fixed points, stability, linear stability
      • Existence, Uniqueness, Picard Iteration, Taylor series methods
      • Blowup, Comparison arguments
    • Elementary Bifurcations on R
      • Saddle Node, Transcritical, Pitchfork bifurcations
      • Normal Forms
      • Stability Diagrams
    • Dynamics on S^1
      • Phase portraits, periodic orbits
      • Bifurcations
      • Asymptotic Period estimates and bottlenecks
      • Compactification of dynamics on R onto S^1
    • Linear Planar Systems
      • Phase portraits, fixed points
      • Fundamental matrix solutions
      • Stability in from Tr(Df) and det(A)
      • linear manifolds E^s, E^c and E^u
    • Planar Systems Introduction
      • Nullclines, Flow, Hyperbolic fixed points
      • Homeomorphisms and Topological Equivalence
      • Liapunov Stable, Attracting, isolated, asymptotically stable
      • Hartman-Grobman Theorem
    • Special Structures in Planar Systems
      • Conservative Systems
      • Hamiltonian Systems
      • Reversible Systems
      • Theorems for Nonlinear Centers
    • Index Theory
      • Definition and Calculation
      • Integral formulation
      • Key properties and Theorems
      • Proving nonexistence of Periodic orbits
    • Periodic Orbits in Planar Systems
      • Conversion to Polar coordinates
      • Limit Cycles and Stability Definitions
      • Gradient Systems - no periodic orbits
      • Dissipative systems - no periodic orbits
      • Liapunov Functions - no periodic orbits
      • Dulac Criterion
      • Poincare-Bendixson Thms (trapping regions)
      • Omega Limit sets, general Poincare-Bendixson.
      • Poincare Return Maps
    • 1-D Maps
      • Euler's method, Newton's method, tent and logistic maps
      • fixed points, stability, asymptotic stability, orbits, cobwebs
      • Linear stability: taylor series and rigorous proofs
      • Introductory examples including superstability
      • Logistic Map: fixed points, period 2, period 3,...

 
 
COVID
POLICY
  

 President Cruzado's 8/26 ruling click here
     

 
 
 LEARNING
 OUTCOMES:
  

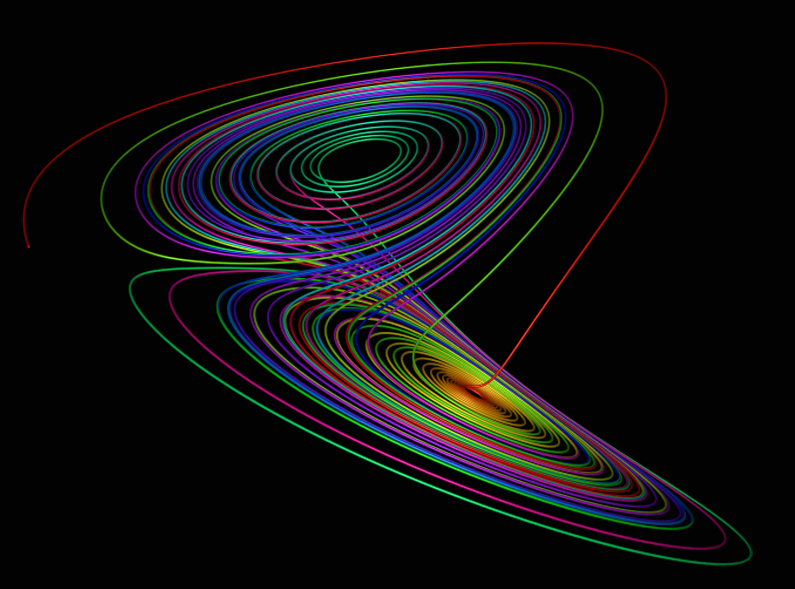
Upon completion of this course, a student will be able to: Provide a qualitative bifurcation analysis of a simple one-dimensional, one parameter nonlinear differential equation; Understand and analyze basic types of linear and nonlinear oscillators; Linearize a two-dimensional non-linear system of differential equations at an equilibrium, and use this linearization to analyze the behavior of nearby solutions; Analyze dynamics of a two-dimensional nonlinear system of differential equations using a phase plane analysis.

Upon completion of this course, a student will be able to: Find fixed points and low period periodic points for simple one-dimensional maps both graphically and analyticaly; Analyze dynamics of one dimensional maps using symbolic dynamics; Understand and be able to reproduce construction of the Smale's horseshoe; Have an understanding of simple models of chaotic dynamics.
   WAGA  

Please inform us of any ADA Web Accessibility issues to the Course Supervisor. Specifically, let us know of any   perceived Section 508 and/or WCAG 2.0 AA issues.