Research
Research interests
And still, many associated research questions have not been answered to full satisfaction, yet. Mathematically speaking, most image processing tasks are instances of inverse problems, where one looks for an underlying, hidden layer of information given a set of derived measurements. New applications, types of images, and questions to be answered through imaging come up everyday. My research interest is to ride on this highly dynamic wave at the cutting-edge frontier of image understanding problems. I want to contribute new mathematical models and efficient schemes for their computation, to provide new and better ways of getting information out of images, and to create new possibilities of imaging in the first place. Taking images is easy. Understanding them is the challenge.
More or less recent projects
This list is by nature always outdated.
Recently the notion of p-Modulus has been extended to families of walks on graphs by Albin, Poggi-Coradini, et al. Here we propose to employ a primal-dual hybrid gradients scheme (Chambolle and Pock) to the greedy algorithm for p-Modulus computation. All optimization steps are simple first order.
We solve the non-linearized and linearized obstacle problems efficiently using a primal-dual hybrid gradients method involving projection and/or L1 penalty. Since this method requires no matrix inversions or explicit identification of the contact set, we find that this method, on a variety of test problems, achieves the precision of previous methods with a speed up of 1-2 orders of magnitude. The derivation of this method is disciplined, relying on a saddle point formulation of the convex problem, and can be adapted to a wide range of other constrained convex optimization problems.
- D. Zosso, B. Osting, M. Xia, S. Osher, An Efficient Primal-Dual Method for the Obstacle Problem (submitted).
preprint
The graph partitioning problem arises frequently in data science, where a graph represents a dataset and the graph partitioning problem is to identify meaningful groups ("clusters") therein. In machine learning, graph partitioning problems arise as data clustering problems, including document classification or community detection in sociological networks, topic modeling, image segmentation, and domain decomposition for scientific computing. The challenges are that the datasets are typically large-scale and high-dimensional and common mathematical formulations of the problem lead to NP-hard problems. Our approach introduces a new measure of optimality for graph partitions, based on the Beltrami energy. The focus of this project is threefold: (i) modeling and in-depth analysis of the graph partitioning problem, (ii) the development of efficient, scalable algorithms, and (iii) translating these algorithms to practical real-world applications.
- D. Zosso, B. Osting, A Minimal Surface Criterion for Graph Partitioning, AIMS Inverse Problems and Imaging, 10(4):1149-1180, 2016. preprint | View at publisher
| 
code - D. Zosso, B. Osting, S. Osher, A Dirichlet Energy Criterion for Graph-Based Image Segmentation, IEEE ICDM 2015. preprint | View at publisher | code
Decomposing a signal into its constituents of different frequency makes these components
accessible for further downstream analysis, such as time-frequency analysis. In the
case of signals defined over multidimensional domains, this decomposition enables
space-frequency analysis, demodulation, estimation of local orientation, edge and
corner detection, texture analysis, denoising, inpainting, or curvature estimation.
Our "Variational Mode Decomposition" model decomposes the input signal into modes
with narrow Fourier bandwidth. We first define the model for one-dimensional signals
(e.g. time-series composed of different oscillations), and then generalize to higher
dimensions. To cope with sharp region boundaries, incompatible with narrow bandwidth,
we introduce binary support functions that act as masks on the narrow-band mode for
image re-composition. L1 and TV-terms promote sparsity and spatial compactness. Constraining
the support functions to partitions of the signal domain, we effectively get an image
segmentation model based on spectral homogeneity. By coupling several sub-modes together
with a single support function we are able to decompose an image into several crystal
grains.
Our efficient algorithm is based on variable splitting and alternate direction optimization;
we employ Merriman-Bence-Osher-like (MBO) threshold dynamics to handle efficiently
the motion by mean curvature of the support function boundaries under the sparsity
promoting terms.
The versatility and effectiveness of our proposed model is demonstrated
on a broad variety of example images from different modalities. These demonstrations
include the decomposition of images into overlapping modes with smooth or sharp boundaries,
segmentation of images of crystal grains, and inpainting of damaged image regions
through artifact detection.
- K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition, IEEE Transactions on Signal Processing, 62(3):531-544, 2014 preprint | View at publisher | code
- K. Dragomiretskiy, D. Zosso, Two-Dimensional Variational Mode Decomposition, EMMCVPR, LNCS 8932:197-208, 2015. preprint | View at publisher | code
- D. Zosso, K. Dragomiretskiy, A.L. Bertozzi, P.S. Weiss, Two-DImensional Compact Variational Mode Decomposition (submitted) preprint
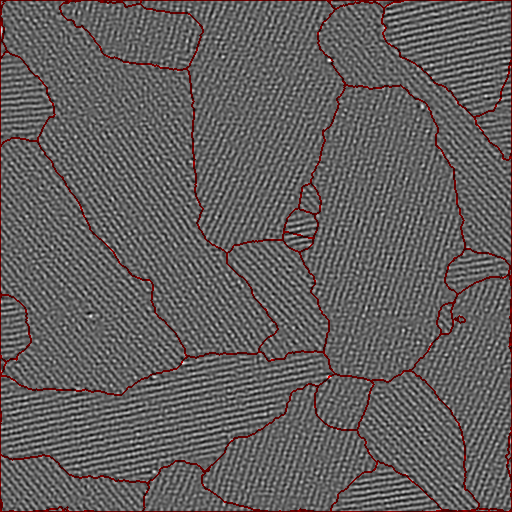
While H1 regularization is known to produce overly smooth reconstructions, the TV (or ROF) model is feature-preserving but introduces staircasing artifacts. The geometrically derived Beltrami framework offers an ideal compromise between feature preservation and avoidance of staircasing artifacts. The main limiting factor of the Beltrami regularizers was the lack of really efficient optimization schemes. Here, we propose an efficient Primal-Dual Projected Gradients algorithm for regularization based on the Beltrami functional. We achieve better performance than ROF denoising for the basic grey-scale denoising problem, then extend the method to more involved problems such as inpainting, deconvolution, and the color case. Therefore, the benefits of the geometric Beltrami regularizer become available at no extra computational cost, compared to state-of-the-art TV/ROF regularizers.
- D. Zosso, A. Bustin, A Primal-Dual Projected Gradient Algorithm for Efficient Beltrami Regularization, 2014. preprint | code
The fundamental assumption in retinex is that the observed image is a multiplication between the illumination and the true underlying reflectance of the object. We define our retinex model in two steps: First, we look for a filtered gradient that is the solution of an optimization problem consisting of two terms: A sparsity prior of the reflectance, such as the TV or H1 norm, and a quadratic fidelity prior of the reflectance gradient with respect to the observed image gradients. In a second step, since this filtered gradient almost certainly is not a consistent image gradient, we then look for a reflectance whose actual gradient comes close. Beyond unifying existing models, we are able to derive entirely novel retinex formulations by using more interesting non-local versions for the sparsity and fidelity prior. Hence we define within a single framework new retinex instances particularly suited for texture-preserving shadow removal, cartoon-texture decomposition, color and hyperspectral image enhancement.
- D. Zosso, G. Tran, S. Osher, Non-local Retinex - A Unifying Framework and Beyond, SIAM Journal on Imaging Science 8(2):787-826, 2015. preprint | View at publisher | code
- D. Zosso, G. Tran, S. Osher, A unifying retinex model based on non-local differential operators, IS&T/SPIE Electronic Imaging, 2013. preprint | View at publisher
Intensity-based image segmentation has essentially been solved by the famous Chan-Vese model. However, this model fails when images are affected by artifacts (scars, scratches) and illumination bias that outweigh the actual image contrast of interest. Here, we introduce a new model for segmenting such damaged images. First, we introduce a dynamic artifact class which prevents intensity outliers from skewing the segmentation. Second, in Retinex-fashion, we decompose the image into illumination and structure. We devise an efficient alternate direction minimization scheme based on variable and operator splitting.
- D. Zosso, J. An, J. Stevick, N. Takaki, M. Weiss, L.S. Slaughter, H.H. Cao, P.S. Weiss,
A.L. Bertozzi, Image Segmentation with Dynamic Artifacts Detection and Bias Correction (submitted) preprint | code
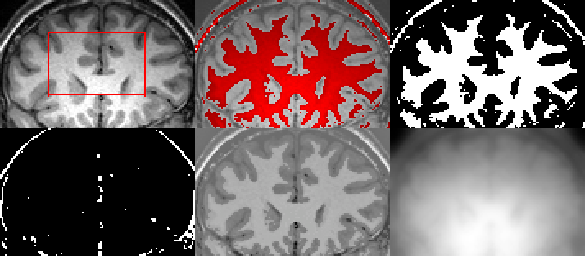
In image registration, one looks for the underlying deformation field that best maps one image onto another. This is a classic ill-posed inverse problem, which is usually solved by adding a regularization term. Here, we propose a multiplicative coupling between the registration term and the regularization term, which turns out to be equivalent to embed the deformation field in a weighted minimal surface problem. Then, the deformation field is driven by a minimization flow toward a harmonic map corresponding to the solution of the registration problem.
The directly resulting minimizing energy flow has poor numerical properties. Here, we provide an efficient numerical scheme that uses a splitting approach: data and regularity term are optimized over two distinct deformation fields that are constrained to be equal via an augmented Lagrangian approach. Overall, we can show the advantages of the proposed FastGAF method. It compares favorably against Demons, both in terms of registration speed and quality.
- D. Zosso, X. Bresson, J.-Ph. Thiran,Geodesic Active Fields - A Geometric Framework for Image Registration, IEEE Transactions on Image Processing 20(5):1300-1312, 2011. preprint | View at publisher
- D. Zosso, X. Bresson, J.-Ph. Thiran, Fast Geodesic Active Fields for Image Registration based on Splitting and Augmented
Lagrangian Approaches, IEEE Transactions on Image Processing 23(2):673-683, 2014. preprint | View at publisher
- D. Zosso, J.-Ph. Thiran, Geodesic Active Fields on the Sphere, ICPR2010, 2010.
View at publisher
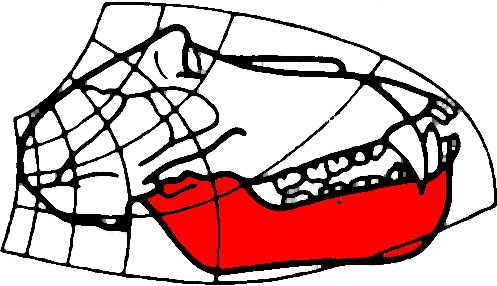
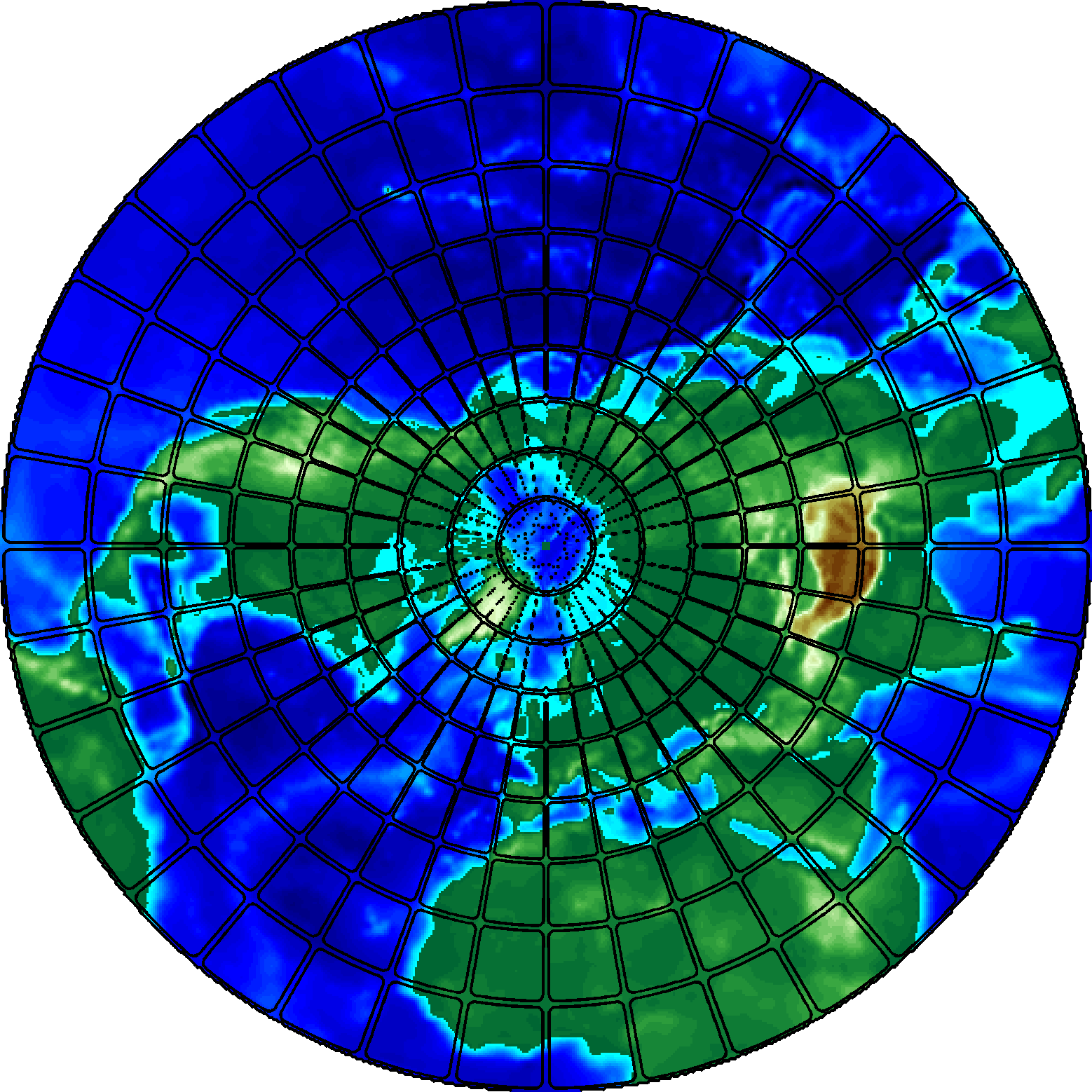
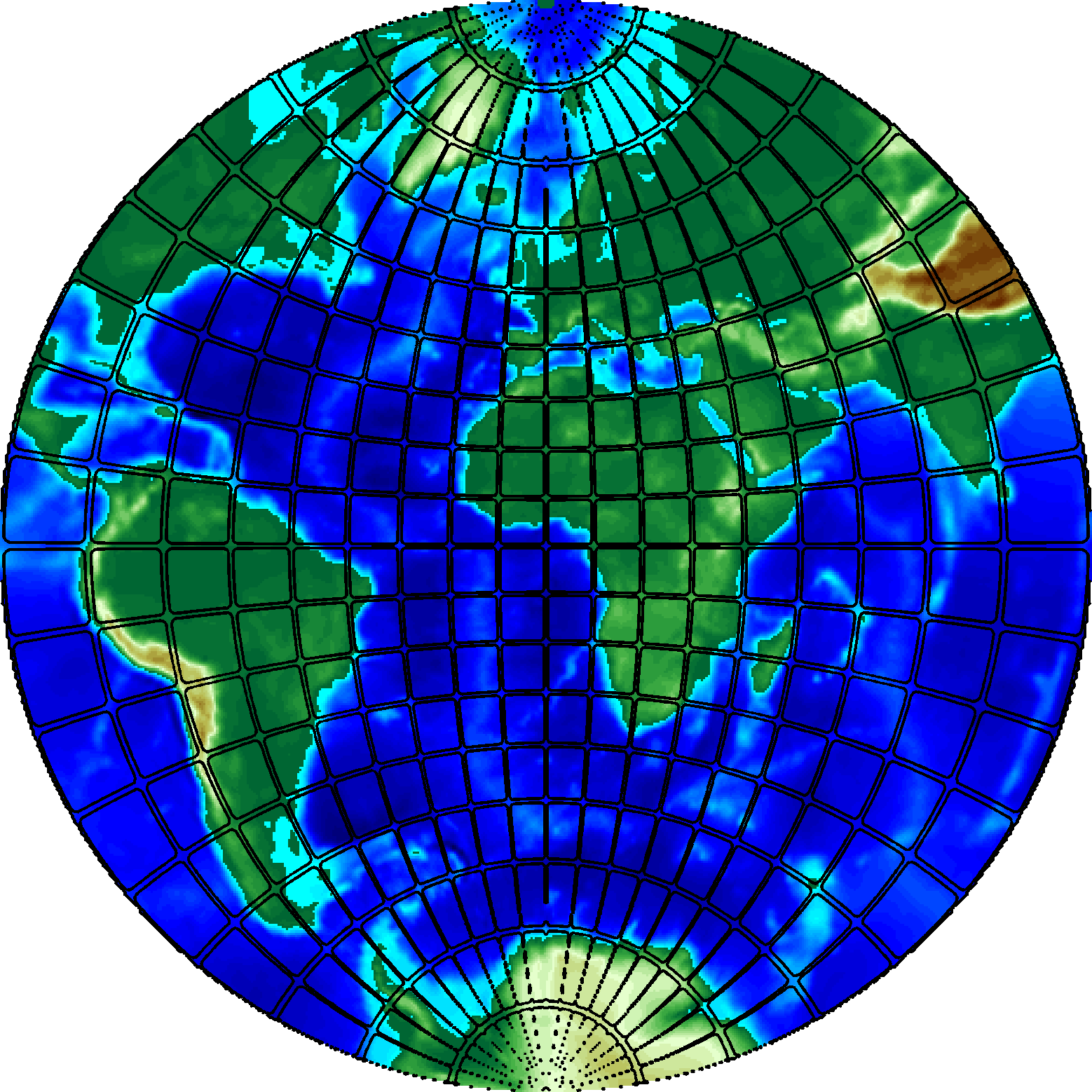
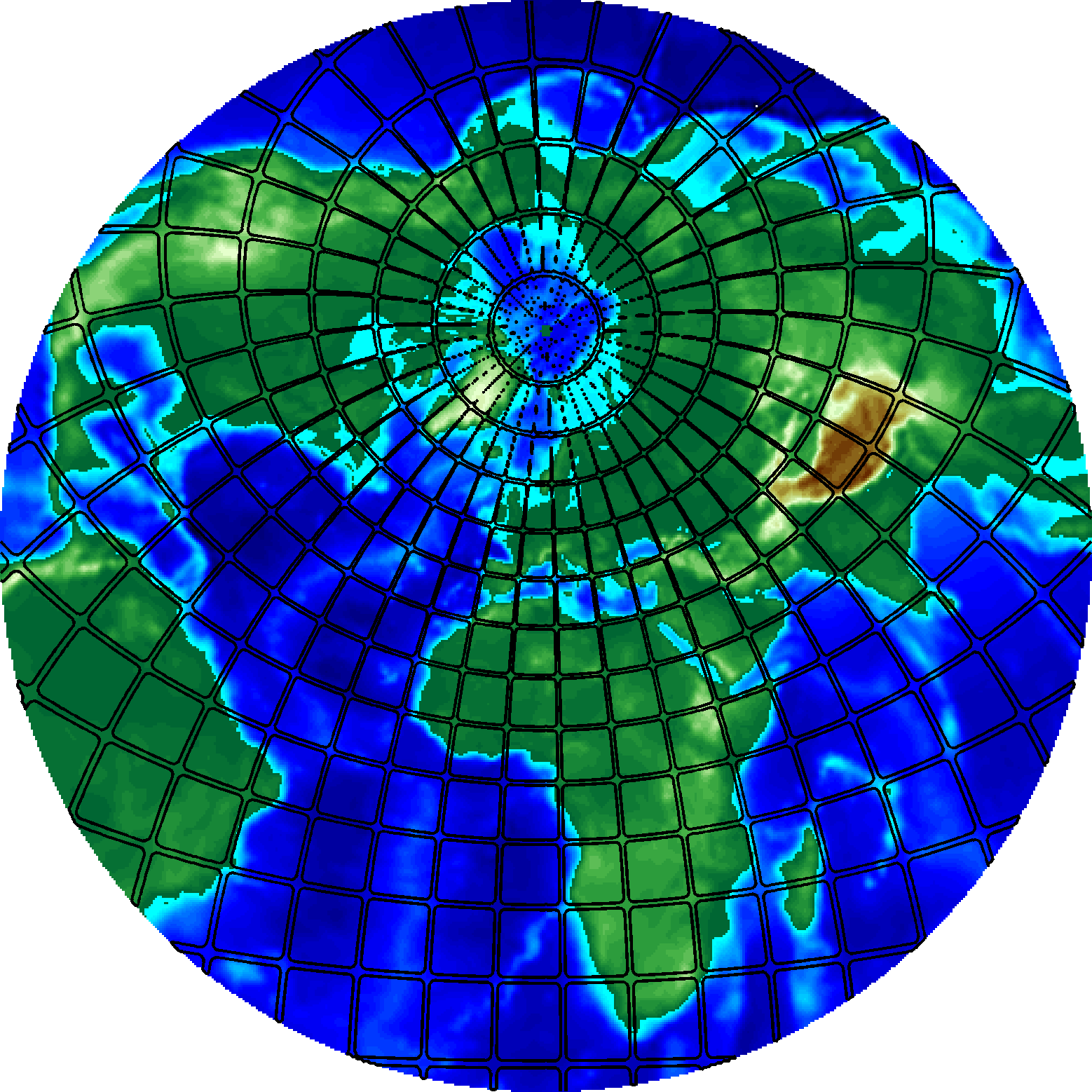
Here, we define a scale-space for cortical mean curvature maps on the sphere, that offers a hierarchical representation of the brain cortical structures, useful in multi-scale registration and analysis algorithms. A spherical feature map is obtained through inflation of the cortical surface of one hemisphere, extracted from structural MR images. Using the Beltrami framework, we embed this spherical mesh in a higher dimensional space and the feature assigned to a mesh vertex becomes an additional component of its coordinates. This enhanced mesh then evolves under Beltrami flow. The collection of all maps produced by this PDE forms a scale-space. Our results suggest that this scale-space provides a generalization of the brain map suitable for use e.g. within a multi-scale registration framework.
- D. Zosso, J.-Ph. Thiran, A Scale-Space of Cortical Feature Maps, IEEE Signal Processing Letters 16(10):873-876, 2009.
View at publisher
