My approach to applied mathematics combines modeling, computation, and analysis to understand problems stemming from general pattern forming systems. Pattern formation is seen in ecological and biological models, chemistry, physics, and even the social sciences. Typical examples are the traveling waves in the Fisher-KPP equation for the transmission of favorable genes or the SIR model for disease epidemics, ringed vegetation patches in desert grasses, hexagon patches in gas discharge experiments, ferrosolitons in ferro-magnetic fluid experiments, and crime hotspot formation. My viewpoint is driven by dynamical systems, and I typically use techniques from spatial dynamics, bifurcation theory, and nonlinear wave propagation.

Overview of Recent Projects

Mathematics of social systems

Paladin Traveling Wave

The unpredictability of human behavior creates many difficulties for mathematicians trying to understand various phenomena that occur in social settings. Game theory provides a strong setting to understand these interactions. Recently, I have been studying variants of an evolutionary, adversarial game that was originally derived to model the formation of cooperation from war torn or crime dominated societies. Including personal relationships and shared ideology can lead to the formation of criminal coalitions, while introducing peer-pressure in a spatial variant can lead to traveling waves of cooperation.

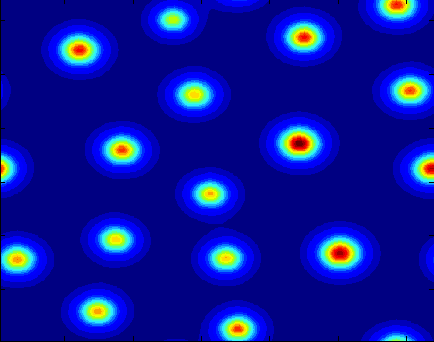
REU Brownian Hotspot
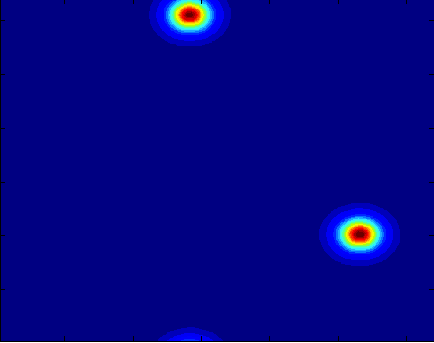
REU Levy Hotspot

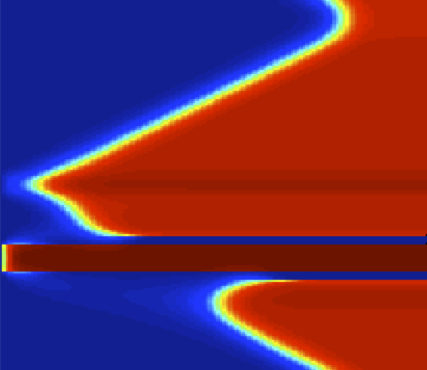
With the help of a team of REU students during the summer of 2012, we studied the effects of allowing criminals to follow a Levy flight, instead of a random walk, on crime hotspot formation. The long jumps associated with Levy flights come about because of the many different methods of transportation a criminal would have. On the right is a hotspot comparison of the agent based model for a random walk (top) and a Levy flight (bottom). The continuum model for these hotspots becomes a nonlocal partial differential equation. The team wrote down the nonlocal model, ran numerical simulations, performed a linear stability analysis, and constructed hot spot profiles in one-dimension in a singular limit.

Radially symmetric spots in the Swift-Hohenberg equation

SH spotSH ring
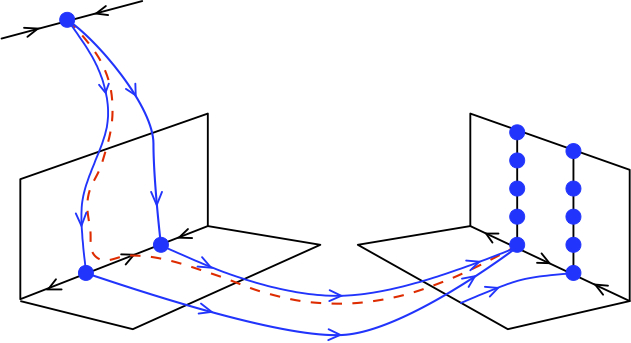
Spot B Geometry

Localized patterns are ubiquitous in nature. In many cases, their formation can be studied as Turing bifurcations in reaction-diffusion equations. The Swift-Hohenberg equation, originally derived to understand the onset of convective roll patterns in fluids experiments, is the normal form in two dimensions to study these bifurcations. Additionally, the Swift-Hohenberg equation supports snaking solution families, where for a fixed range of parameter values an infinite family of localized roll patterns exist, all connected in bifurcation space. These solutions vary by their number of localized rolls.

In order to understand these patterns in various dimensions, we treated the dimension as a continuous parameter and explored the bifurcations curves of these solutions. As an unexpected result, we found another spot solution. We then rigorously proved the existence of these spots at onset in two and three dimensions using a geometric framework that does not rely on an a priori understanding of the spot's amplitude scaling.