JRSSB Paper
% Some results that compare Fox's Laplacian precision matrix (= inv(exponential% covariance) via FEM method%% to%% Higdon's Laplacian precision matrix (= '1st order locally linear')%
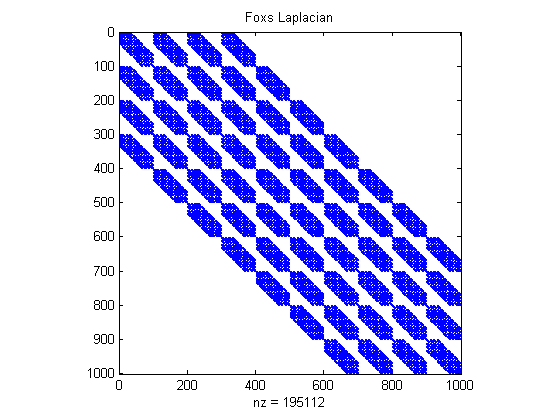
% Using Colin's 3d inv(Exp) using FEMprec% The .25 is 1 over correlation length, Colin says to use 1/4 clear all [H p]=FEMprec(.25,9); Omega_fox=H*p*H; % Precision matrix for prior for phi, phi ~ N(0,constant*inv(Omega_fox)) figure(1);clf spy(Omega_fox) % There are 195K non-zeros in this matrix title('Foxs Laplacian') % When second param in FEMprec is 9, then A1 is a 1000 x 1000 precision matrix% When second param in FEMprec is k, then A1 is a (k+1)^3 x (k+1)^3 precision matrix
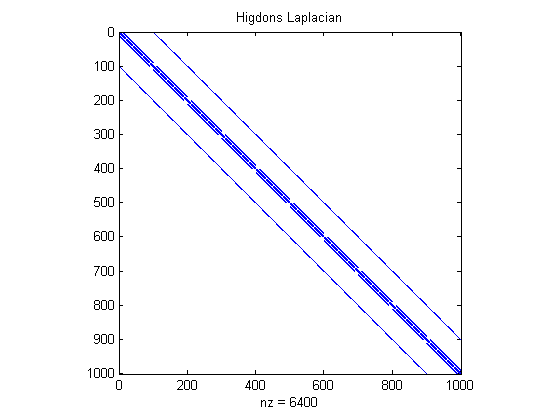
% Using Higdon's 1st order locally linear precision matrix Omega_hig = GetCovMRFsparse_n3_3d(10,0); % Another candidate precision matrix for prior for phi, phi ~ N(0,constant*inv(Omega_hig)) figure(2);clf spy(Omega_hig) % There are 195K non-zeros in this matrix title('Higdons Laplacian') %
Checking BOTTOM face ...Elapsed time is 0.001670 seconds. Checking SOUTH face ...Elapsed time is 0.003225 seconds. Checking EAST face ...Elapsed time is 0.009229 seconds.
n = length(Omega_fox) %1000 x 1000 vert = round(n^(1/3)); %%%%%%%%%%%%%%%%%%%%%%%%%% Now scale the precision matrix by max(A1(:)) Omega_s_fox = Omega_fox/max(Omega_fox(:));
n =
1000
% Model%% y = F*\phi + \epsilon,%% \epsilon ~ N(0,inv(g_eps*eye(n)))% \phi ~ N(0,inv(g_phi*Omega))%% The matrix F models the linear measurement process. Keep it simple for this% exercise, let F trivially be the identity F=sparse(eye(n)); m=n;
%%%%%%%%%%%%%%%% Posterior for phi = biofilm image | y=noisy image;% phi|y ~ N(g_eps*inv(A)*F'*y, inv(A))
% Posterior precision matrix for p g_eps = 1; g_phi = 1; % Put a lot of weight on prior for a smooth reconstruction A_fox = g_eps*(F'*F) + g_phi*Omega_s_fox; % precision matrix of posterior for phi A_hig = g_eps*F'*F + g_phi*Omega_hig; % precision of posterior for phi bio_ellipse = MakeEllipseWFlatBottom([.2 .2 .55]*vert,vert,.3*vert,1); % An ellipsoidal column of biofilm
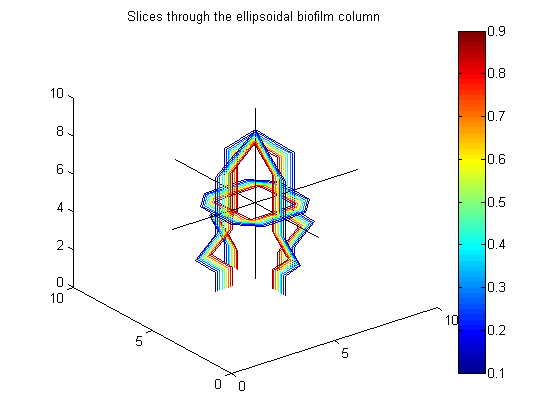
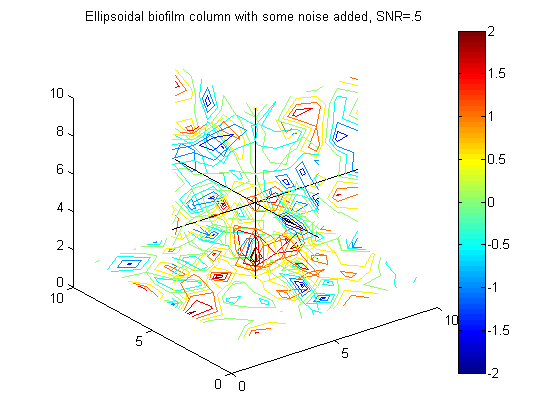
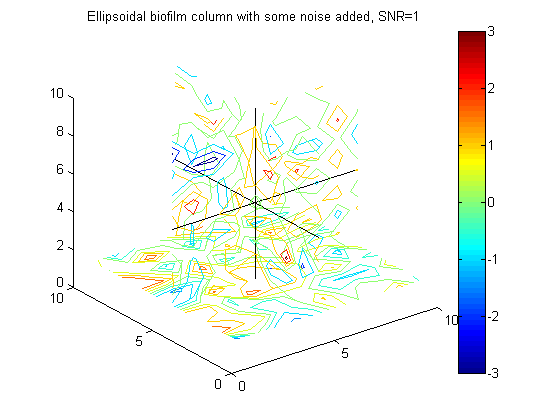
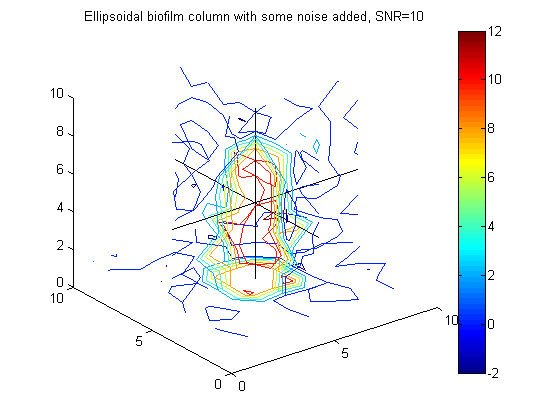
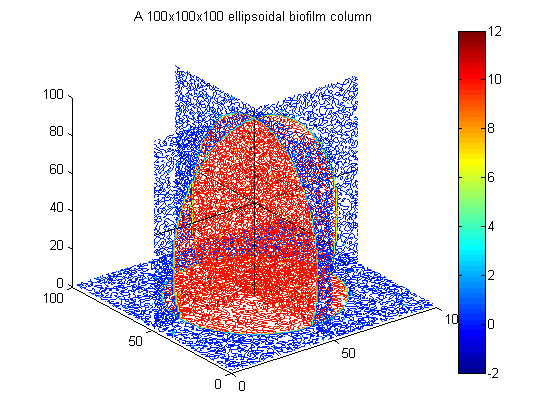
% Example to go in paper big_vert=100; big_bio_ellipse = MakeEllipseWFlatBottom([.4 .4 .65]*big_vert,big_vert,.3*big_vert,0); % An ellipsoidal column of biofilm figure(20);clf;contourslice(10*big_bio_ellipse+randn(100,100,100),[big_vert/2],[big_vert/2],1); view(3) title('A 100x100x100 ellipsoidal biofilm column') colorbar hold on plot3([1 big_vert],[big_vert/2 big_vert/2],[big_vert/2 big_vert/2],'k') plot3([big_vert/2 big_vert/2],[1 big_vert],[big_vert/2 big_vert/2],'k') plot3([big_vert/2 big_vert/2],[big_vert/2 big_vert/2],[1 big_vert],'k')
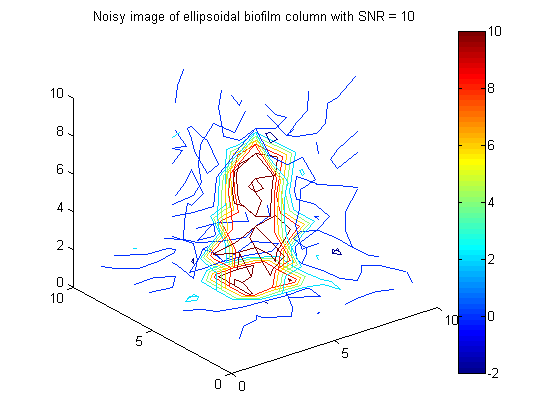
% Generate 10x10x10 image, y = F*phi + \epsilon, where phi is ellipsoidal column of biofilm y = 10*(F*bio_ellipse(:)) + 1/sqrt(g_eps)*randn(m,1); % Generate data .... SNR = 10 figure(6);clf;contourslice(reshape(y,vert,vert,round(m/vert^2)),[vert/2],[vert/2],1); view(3) title('Noisy image of ellipsoidal biofilm column with SNR = 10') colorbar
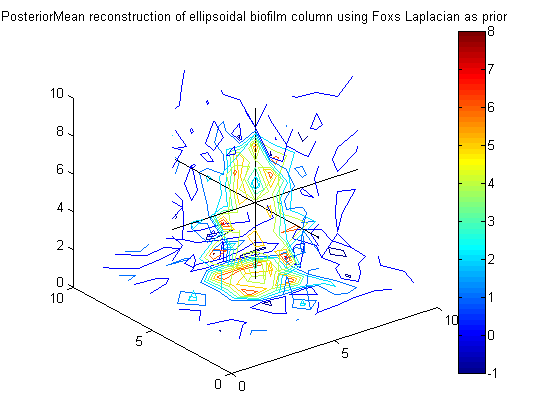
% Calculate posterior mean for phi using Foxs% Laplacian as prior precision,% PosteriorMean_fox = A_fox \ (g_eps*(F'*y)); figure(7);clf;contourslice(reshape(PosteriorMean_fox,vert,vert,vert),[vert/2],[vert/2],1); view(3) title('PosteriorMean reconstruction of ellipsoidal biofilm column using Foxs Laplacian as prior') colorbar hold on plot3([1 vert],[vert/2 vert/2],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[1 vert],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[vert/2 vert/2],[1 vert],'k')
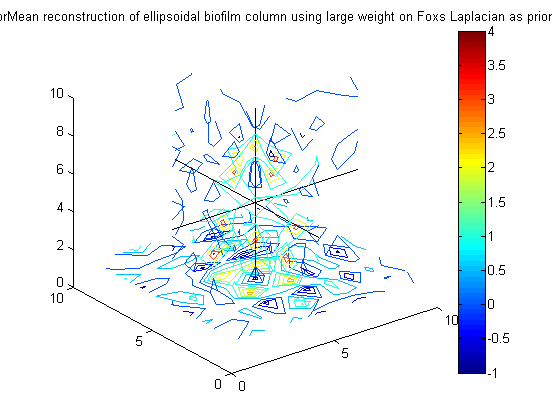
% Get same non-smooth behavior for different values of R = correlation% length and even for large weighting on prior, get A_fox10 = g_eps*(F'*F) + 10*g_phi*Omega_s_fox; % precision matrix of posterior for phi PosteriorMean_fox10 = A_fox10 \ (g_eps*(F'*y)); figure(21);clf;contourslice(reshape(PosteriorMean_fox10,vert,vert,vert),[vert/2],[vert/2],1); view(3) title('PosteriorMean reconstruction of ellipsoidal biofilm column using large weight on Foxs Laplacian as prior') colorbar hold on plot3([1 vert],[vert/2 vert/2],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[1 vert],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[vert/2 vert/2],[1 vert],'k')
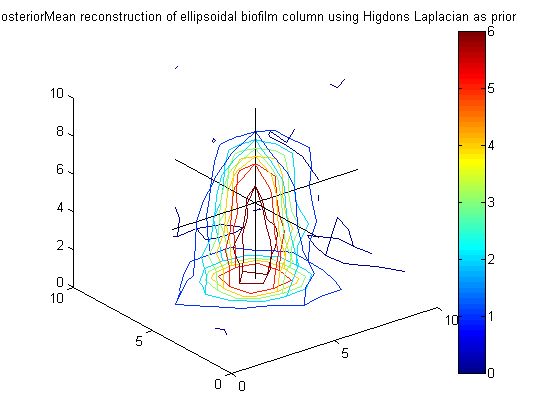
Calculate posterior mean for phi using Higdons Laplacian as prior precision, get smooth reconstruction as anticipated
PosteriorMean_hig = A_hig \ (g_eps*(F'*y)); figure(8);clf;contourslice(reshape(PosteriorMean_hig,vert,vert,vert),[vert/2],[vert/2],1); view(3) title('PosteriorMean reconstruction of ellipsoidal biofilm column using Higdons Laplacian as prior') colorbar hold on plot3([1 vert],[vert/2 vert/2],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[1 vert],[vert/2 vert/2],'k') plot3([vert/2 vert/2],[vert/2 vert/2],[1 vert],'k')
% Get a Cholesky sample Q_fox = chol(A_fox); % A = Q'*Q, inv(A) = inv(Q)*inv(Q') xc_fox = Q_fox\randn(n,1) + PosteriorMean_fox; vert=round(n^(1/3)); figure(9);clf;contourslice(reshape(xc_fox,vert,vert,vert),[vert/2],[vert/2],1); view(3) colorbar title('Cholesky sample from posterior using Foxs Laplacian as prior')
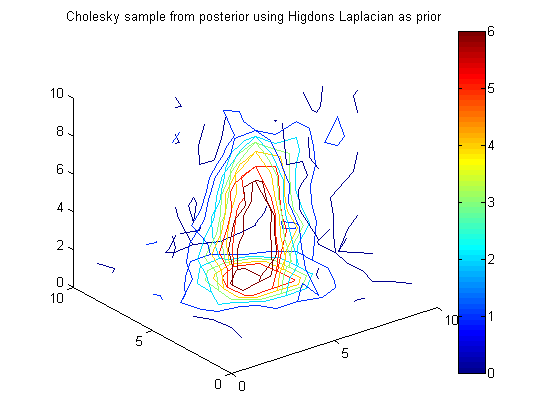
% Get Cholesky samples Q_hig = chol(A_hig); % A = Q'*Q, inv(A) = inv(Q)*inv(Q') xc_hig = Q_hig\randn(n,1) + PosteriorMean_hig; figure(10);clf;contourslice(reshape(xc_hig,vert,vert,vert),[vert/2],[vert/2],1); view(3) colorbar title('Cholesky sample from posterior using Higdons Laplacian as prior')