Research

My research interests originated in the area of Sensitivity Analysis. I am interested in the design, development and implementation of computational methods for sensitivity calculations. Sensitivities quantifiy how small changes in parameter values influence the solutions to ordinary or partial differential equations.
What is a sensitivity? Mathematicians and other scientists model physical systems using a set of mathematical equations --- these might be algebraic equations or ordinary differential equations or even partial differential equations. These equations will describe how some STATE VARIABLE such as temperature, velocity, pressure or population changes over time. Inevitably, there are also PARAMETERS floating around in the models. These parameters might describe physical properties such as thermal conductivity, permeability, porosity, birth and death rates, parameters that describe the shape of an airfoil or an airplane wing, parameters that describe the position of sensors and actuators within a control system on a MAV, etc. The sensitivity describes how small changes in a parameter value affect the state variables. In short, a sensitivity is a derivative ; it's the rate of change of the state variable per unit change in the parameter value.
How does one compute a sensitivity? There are many ways that scientists attempt to compute sensitivities, and it varies largely with the application that one is considering. My early research focused on the use of Continuous Sensitivity Equation Methods (CSEMs). This approach begins by "differentiating" the mathematical model in order to derive an equation (or a set of equations) for which the sensitivity is a solution. This equation is called the SENSITIVITY EQUATION, and deriving, solving, analyzing and approximating sensitivity equations was the focus of my research for several years. More recently, I am interested in using techniques from the field of uncertainty quantification (UQ) to compute sensitivites and evaluate the usefulness of models.
How might one use a sensitivity? Sensitivities provide for a direct gradient calculation in some optimal design problems where the constraints are defined by PDEs. They can also be used for parameter prioritization in model analysis, and some of my colleagues have used them in the quanitification of uncertainty in models. For the most part, I am referring to models of a large variety of engineering systems.
Current Research
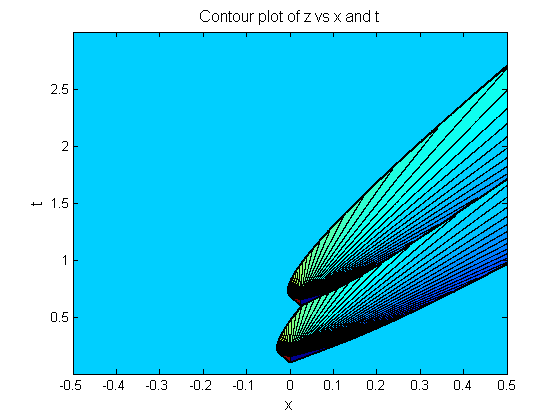
One of my current research projects involves the study of mathematical models used to describe transcription processes in bacteria, such as E. coli. One of the models is a stochastic model related to the TASEP models that are often used in the literature. Another model of interest is a nonlinear hyperbolic PDE in conservation law form. The basic equation was once suggested as a model for traffic flow in the 1950's. Jennifer Thorenson used Discontinuous Galerkin Methods to simulate various versions of the model as we try to incorporate realistic biological features such as density dependent velocities and transcriptional pauses. Experimental data suggests that certain types of transcriptional pausing are present in certain types of genes, and it has been hypothesized that the pauses serve as a regulatory mechanism to balance transcription and translation to optimize protein production by the cell. Jennifer's project investigated the effect that these pauses have on overall protein production via the proxy of transcription rate measurements. Both location and time duration of pauses influenced overall transcription rates, and promoter occlusion was observed in the model simulations for various parameter choices. Upon tuning the model for realistic experimental data, a statistical analysis was performed in order to quantify tradeoffs for various parameter choices.
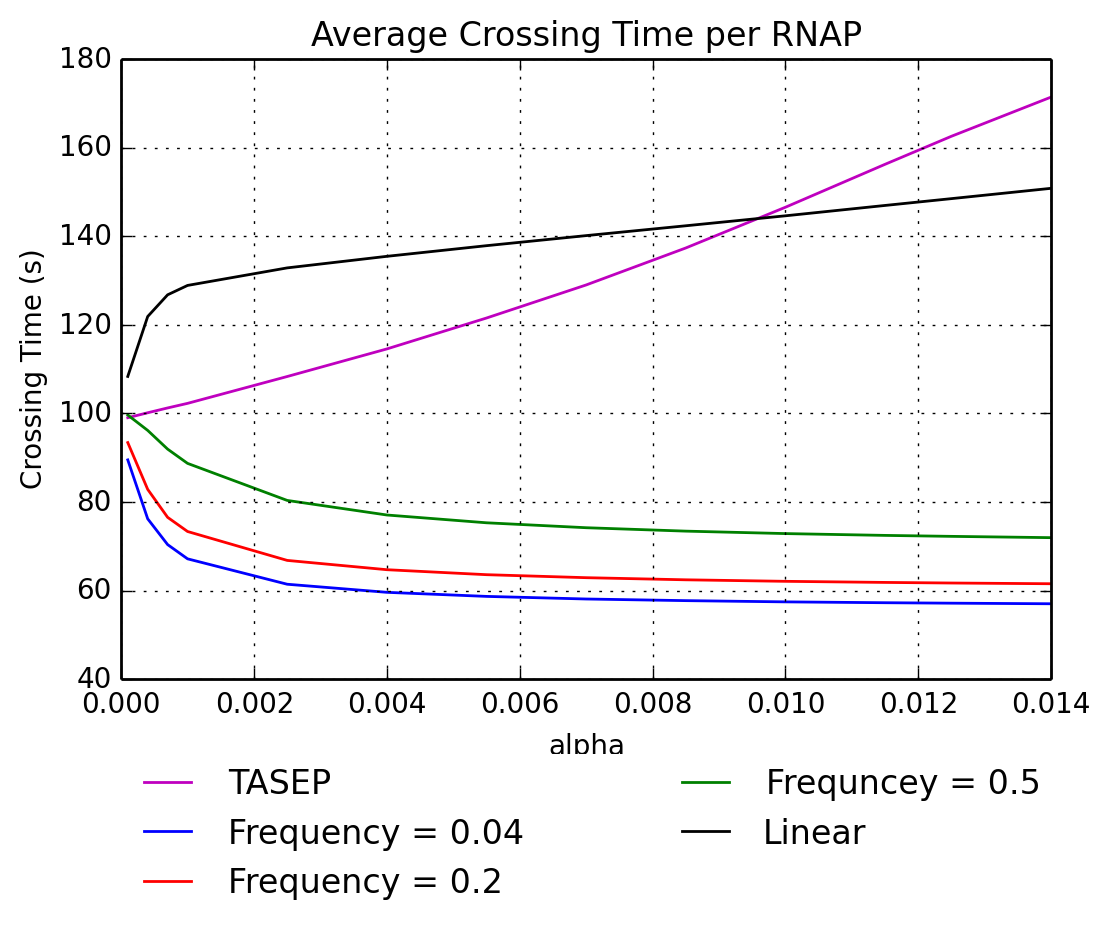
Tamra Heberling explored a stochastic model for transcription which is based on the popular TASEP model, and she added torque effects to the basic stochastic model. The torque effects accounted for torsional forces imparted on the DNA strand by RNAPs during transcription. Model simulations indicate that when the density of RNAPs increases, the average transcription time per RNAP actually decreases. We hypothesize that this is due to the torque effects being harnessed by the RNAPs in order to cooperatively increase elongation rates of their transcriptional neighbors. Future research areas include the incorporation of techniques from the field of uncertainty quantification in order to better understand how various parameters related to transcriptional pauses and other biological factors influence the overall transcription rates, protein production rates and ultimately, cell fitness.
Undergraduate Students

Zach Dupree

Garret Vo

Katelyn Weber
Katelyn graduated in Spring of 2013. She was funded through the Undergraduate Scholars Program and the Montana INBRE program to perform an uncertainty analysis on a mathemtical model of RNAp transcription that includes the presence of short, frequent transcriptional pauses. The RNAp transcription time or crossing time, is the average length of time it takes the RNAp to transcribe an entire strand of DNA. She studied the variations of average transcription time per polymerase based on the uncertainty in RNAp transcription rates and in the randomness of pause locations and durations. Katelyn applied statistical techniques that use a collection of parameter inputs (instantaneous transcription speed, number of pauses and duration of these pauses) to estimate a region of parameter space that corresponds to the RNAp crossing time of 60 seconds (which has been reported in the literature). The variability of the average crossing time per affected polymerase was investigated given various pause frequencies and durations. An upper bound on the variability of crossing time was estimated from the random variables, both theoretically and through simulations.
Graduate Students

Tamra Heberling (2016)
Tamra's research is in the area of model development and computation. She is currently
developing a model to understand the effect of torque (exerted on it by its neighbors)
can affect the transcriptional velocity of a polymerase transcribing a DNA strand.
A paper published in Science in 2013, Transcription Under Torsion by Jie Ma et al,
was an inspiration for this project. In this paper, they were able to show experimentally
that the torque exerted on the polymerase can hinder its movement and cause it to
stall while it is transcribing the DNA strand. Interestingly, the torque can also
contribute to the velocity of the polymerase if it is helping to unwind the DNA strand.
Ultimately, she developed a mathematical model that uses these forces to generate
the pauses that occur during transcription, and determine the effect they have on
the transcription rate. Her work showed that torsional effects could explain why certain
types of genes display increases in transcription rates when the gene is occupied
with a large number of RNAPs simultaneously. This behavior was observed experimentally
by Epstein and Nudler, and the RNAPs were thought to be cooperating in order to increase
elongation rates. Tamra's model showed that torque effects is a mechanism that RNAPs
could harness in order to achieve this type of cooperation.

Dr. Jennifer Thorenson (2013)
She is currently an instructor at the University of Oregon in Eugene, OR. In her thesis work, she used the classical traffic flow PDE from the 1950s to model the biological process of transcription; the process of transferring genetic information from DNA to mRNA, in an E. coli gene. Polymerase elongating along the DNA strand encounter frequent but short pauses which are incorporated into the transcription model as several traffic lights. These pauses result in a delay in the transcription time and a delay function is defined to quantify this effect. Numerical simulations of the PDE model were conducted using a discontinuous Galerkin finite element method (DG) formulation. The entropy satisfying weak solution of the PDE model with a single pause is derived using the method of characteristics. This weak solution was used to show convergence of the DG formulation even though the flux function is not smooth. Once convergence of the DG solution was established for one pause, the numerical simulation for multiple pauses is used to calculate the delay due to the pauses and determine their effect on the overall transcription time. Preliminary parameter studies show a complex relationship between pause location and delay values.
