blue line

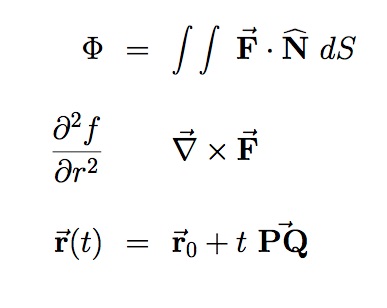                   title 1  title 2

blue line

        Instructor  
  Mark Pernarowski
            pernarow @ montana.edu
            Schedule (Wil 2-236)
        Textbook  
We will use the following two free (web) textbooks
               CLP-3 - Multivariate Calculus
               CLP-4 - Vector Calculus
             At the textbook website you can also download a PDF version.
        Classroom  
NAH 337  (MTRF 11:00-11:50)

 blue line

 

  

 

Grading: The course % is determined by:

   Midterm 1      M1           100 
   Midterm 2      M2           100
   Final                F               100
   Quizzes           Q             100
  ________________________________
                                            400

         % = (M1+M2+F+HW)/4
 
The final is not comprehensive.
Six quizzes each worth 20 points
will be given. Your best 5 quiz
scores determine Q above.

Exam and quiz dates are indicated
below. Their content will be announced in class.

All exams and quizzes are closed book and no electronic devices are permitted.

Grades will be recorded in D2L

Syllabus: Will evolve as the course develops. See the linked material below.

Homework: Suggested homework is listed below.

Although the homework is not graded
it is representative of the kinds of
questions which will be on quizzes
and exams.

Some additional problem sets and/or
review sheets will be posted later on this site.

Links:

 

 

 

blue line

 

Schedule Anticipated schedule for quizzes (orange), tests (red) and holidays (green).
                   
 Sunday     Monday Tuesday Wed Thursday Friday Saturday
20          
21
22
23
 
24
 
25
 26
27
 		 28
29
30
31
1          (Q1)
 2
 
3
 
4
Labor Day
5
 6
7
8
 9
 
10
 
11
12
 13
14
15       (Q2)
 16
 
17
18
19
 20 21
 Review

22
Midterm 1

23
24
25
26
 
 27
28
 
29
 
 30
 
1
 
2
 
 3 4
5
 
6          (Q3)
 
 7
 
8
 		 9 10
11
 12
13
 14
 
15
 
16
17
18
19
20       (Q4)
 21
22
 		 23

 24

 25

 26
 Review		 27
Midterm 2
 28
 
29
 
30
 
 31

 1

 2

 3

 4
 
5
 		 6

 7

8
9         (Q5)
 10  
Vet. Day		 11
 
12
 
13
 
14
 
 15
16
 
17
 18
 
19
 
20
Thanksgivin
21  
Thanksgivin
22
Thanksgivin
 23
Thanksgivin		 24
Thanksgivin
 25
26
27
 
28
 
 29
 
30
 1         (Q6)
 2
3
4
 
5
 

6
7
8
Review
 9
10
11
Finals
12
Finals

 13
Final Exam
10-11:50am

14
Finals

15

 16

 

 blue line

Suggested Homework and Syllabus

 

1.1
Points
 
1.1
Exercises - Stage 1
2,3,4
1.2
Vectors
 
1.2.1
Vectors: Addition and Scalar Multiplication
 
1.2.2
Vectors: Dot Products and properties
 
1.2.4
Vectors: Cross Products and Properties
 
1.2.6
Vectors: Vector Identities
 
1.2.9
Exercises - Stage 1 
3,4a,5b,6,7,16,18a,21a,21d,23b,25,27
1.4
Equation of Planes in 3d
 
1.4
Exercises - Stage 1
3,5,7a,8a,10
1.5
Equation of Lines in 3d
 
1.5
Exercises - Stage 1
4,5,6
1.6
Curves and Their Tangent Vectors
 
1.6.2
Exercises - Stage 1,2
2,5,7,10,11a,12,13,20
 
 
 
 
Midterm 1 (9/22)
Review Problems for Midterm 1
 
 
 
1.7
Graphs, Surfaces, Level Curves, Level Surfaces
 
1.7.2
Exercises - Stage 1
4,7a,9,12 (optional)
2.1
Limits
 
2.1.2
Exercises
3,6a,6b,6c,8,10
2.2
Partial Derivatives
 
2.2.2
Exercises
4a,4b,6
2.3
Higher Order Derivatives
 
2.3.3
Exercises
3a,3b,5a (has a trick), 5c
2.4
Chain Rule
 
2.4.5
Exercises
1,6,15,16
2.5
Tangent Planes
 
2.5.3
Exercises
1,5,6,7,8,11
2.6
Linear Approximations
 
2.6.1
Quadratic Approximations (optional)
 
2.6.3
Exercises
3, 4,11
2.7.1
Directional Derivative and Gradient
 
2.7.2
Exercises
3,7,11,12,17,22(hard),29a,b
2.8
Partial Differential Equations - SKIP
 
2.9
Maximum and Minimum Values
 
2.9.3
Exercises
1a,6,7,9,16a,28
2.10
Lagrange Multipliers
 
2.10.2
Exercises
1,3,5,7,8,11,15b,23,24
 
 
 
 
Midterm 2 (10/27)
Review Problems for Midterm 2
 
 
 
3.1
Double Integrals
 
3.1.7
Exercises
1a,b; 2b,d; 3a-c, 4a-c,5,8,13
3.3
Integral Application
 
3.3.4
Exercise (may need integral tables)
7
3.5
Triple Cartesian Integrals
 
3.5
Exercises
3,4,10,11,18a
3.2
Polar Integrals
 
3.2.5
Exercises
1,5a-d,6a,7,8,9
3.6
Cylindrical Integrals
6,7,9 (above z+x^2+y^2)
3.7
Spherical Integrals
7b,8,10a
3.4
Surface Area (of graphs only - Eqn 3.4.1)
4,5,6,10 (convert to polar)
 
 
 
 
For the following, Exercises are from either the indicated CLP-3 - Multivariate Calculus textbook or the CLP-4 - Vector Calculus textbook.
 
 
 
 
2.3
Conservative Vector Fields ( CLP-4 - Vector Calculus)
6,7,8
2.4
Line integrals ( CLP-4 - Vector Calculus)
10a, 13, 16,25a-c
3.3.2
Surface integrals on graphs ( CLP-4 - Vector Calculus)
4,5,6,9,16c,23,24
 
 
 
 
Final (12/13 @ 10am-11:50am in our classroom)
Review Problems for Final
 
 
(exclude Divergence Theorem)

 blue line

Review Material for Exams

  Review Problems for Midterm 1  Midterm 1 (Friday, Sept 22)
  Review Problems for Midterm 2  Midterm 2 (Friday, Oct 27)
  Review Problems for Final  Final (Wednesday Dec 13)

 

 blue line

Quiz Outline

 

       Content Description
Quiz 1

9/1

Quiz is vectors/dot products(25 min - no electronic devices). 

  • vectors - addition, subtraction, notation, magnitude, unit
  • Dot Product
    • computing dot products
    • angles between vectors (angles at triangle vertices)
    • when are vectors orthogonal (normal) 
    • projection of one vector onto another
Quiz 2
9/15

Quiz on cross products, lines, planes (25 min - no electronic devices)

  • Lines in R3
    • vector and parametric equations
    • finding equations of lines
      • through 2 points
      • thru a point and with a given direction
      • a line parallel to some other line
    • knowing when two lines are parallel
    • Finding point of intersection for intersecting lines
  • cross product - how to compute, how to find vectors perpendicular to others, areas of triangles, identity  ||u x v || = || u || || v || sin(theta)
  • equations of planes: from 3 points, a point and a line, parallel and intesecting lines, points and normal vector N
  • angles between intersecting planes and between lines that intersect a plane
  • distance between points and a plane, and between parallel lines
  • no questions on curves in space (1.6)
  • no questions on graphs of functions z=f(x,y)
Quiz 3
10/6

Quiz covers topics in 2.1-2.7 of text with a de-emphasis of the proofs and detailed theory:

  • proving limits DNE (do not exist) by showing limits on different paths of approach differ
  • evaluating limits when they do exist
  • Computing partial derivatives (first and second order)
  • Tangent planes to graphs of f(x,y), normal vectors and Linear approximations
  • Gradients: definition and calculation of.
  • Chain Rule for Paths
  • Directional Derivatives
  • Maximal rate of change = gradient direction
  • Gradients: as normal vectors to level sets
  • Finding normal vectors to level surfaces g(x,y,z)=c and associated tangent planes
Quiz 4 10/20

Quiz is on some of 2.4, most of 2.9 and non-word problems of 2.10.

  • Chain rule problem like 2.4#6 where f=f(x,y) and x=x(s,t),y=y(s,t)
  • Finding critical points
  • Classifying critical points using the Second Derivative test
  • NO problem maximizing/minimizing over a bounded region.
  • Lagrange muliplier method for (simple) functions of two variable:
  •                     extremize f(x,y) over the set g(x,y)=0.
  • Simple Lagrange muliplier method for (simple) functions of three variables:
  •                     extremize f(x,y,z) over g(x,y,z) = 0
  • NO optimization word problems.
Quiz 5 11/9

There will be 4 questions:

  • Evaluating a double cartesian integral. May need u-substitution.
  • Reversing order of integration - double integral.
  • A simple cartesian triple integral - set up only
  • Setting up a polar integral - dA=r dr d\theta , x=r cos \theta, y=r sin \theta
Quiz 6 12/1

There will be 4 questions: HW FOR IS MARKED IN GREEN ABOVE-Harder problems.

  • Set up a Triple integral in cylindrical coordinates
  • Set up a Triple integral in spherical coordinates
  • Compute a Vector line integral
  • Compute a Vector line integral of a Gradient vector field (potential function)

 
     
     
     
     

 

Exam Outlines
Midterm 1 9/22

 50min, No electronic devices, no notes, no formula sheet

  • recommended HW questions and the Review Sheet  especially are accurate representations of the kind of Midterm questions-- although there will NOT be a question like Review Sheet (1) or (8e). A coarse summary of topics are below:
  • dot and cross product properties and identities
  • equations of lines and planes (big topic)
  • velocity, speed, acceleration, arclength
  • unit tangent, tangent line, planes orthogonal to curves
  • textbook sections: 1.1,1.2,1.4,1.4,1.5,1.6
     
   

 
Midterm 2 10/27
Textbook Sections: 1.1,1.2,1.4,1.5,1.6
    
    1. Showing limits DNE or evaluating when one knows they exist
    2. Computing partial derivatives of first and second order
    3. Tangent planes/lines to: f(x,y)=c, z=f(x,y) and g(x,y,z)=c
    4. Linear approximations z=L(x,y) to z=f(x,y) at (a,b)
    5. Gradients and Directional derivatives (geometry & properties)
    6. Chain Rules: on paths  z=f(x(t),y(t)) and for z=f(x(s,t),y(s,t))
    7. Normal vectors for: f(x,y)=c, z=f(x,y) and g(x,y,z)=c
    8. Critical points and Second derivative Test
    9. Method of Lagrange Multipliers: extremize f(x,y) and/or f(x,y,z) subject to at most one constraint.
  • 25% of the exam may be on Lagrange multipliers for
    problems of 2 or 3 variables (and one constraint), i.e f=f(x,y) or f=f(x,y,z), etc.
    Possibly a simple word problem.
  • 25% of the exam will be a find and classify critical point problem.
  • There WILL be a question on Item 7 above. Make sure you know this one!!
  • There will be a Chain Rule question.
  • Balance will be taken from the rest in the list above
  • Notable Exclusion: There will be NO problems involving maximing f(x,y) on a region like (7) in the Review Sheet posted here. Also, there will be no Directional derivative question.
     
     
     
Final Wed 12/13 10-11:50am,  Location: NAH 337 (our classroom)
   
Will cover: TBA
  • Review Problems for Final : indicative problems
  • You have 1hr 50min but I'm trying to write a 75min exam.
  • There will be 9-10 questions. Some should be easy.
  • you'll be required to evaluate about half the integrals. The rest you will only be required to "set up" the integrals

You may find the following information formula sheet helpful but it includes a few things we didn't have time to cover: formula sheet.

Specific Topics:

  • double integrals in cartesian coordinates
  • reversing the order of integration on a double integral
  • double integrals in polar coordinates
  • triple integral in cartesian coordinates
  • triple integral in cylindrical coordinates
  • triple integrals in spherical coordinates
  • scalar line integrals
  • Vector line integrals
  • line integrals of conservative vector fields - know curl (F)=0 means F conservative
  • surface integrals (graphs z=f(x,y) only)
  • flux integrals (graphs z=f(x,y) only)
  • Divergence Theorem

Notable exclusions:

  • parametrized surfaces
  • Stokes Theorem
  • Greens Theorem

LEARNING

OUTCOME

  

 Be well versed in multivariate differential and integral calculus

 

 WAGA

  

Please inform us of any ADA Web Accessibility issues to the Course Instructor. Specifically, let us know of any perceived Section 508 and/or WCAG 2.0 AA issues.